Весёлое Скалярное произведение векторов и его свойства
Скалярное прозведение векторов — штука вроде простая, но не особо понятная. Куда ни зайдешь — везде много формул, и всяких дурацких терминов. А в итоге запоминашь как оно делается и решаешь две три задачки на экзамене и всё. Если повезет столкнуться с аналитической геометрией в более осознанном возрасте проблема остается той же самой. Не понятно ни что это, ни как это применять.
На простых примерах я постараюсь объяснить главное — в чем геометрический смысл этой штуки, какими свойствами это произведение обладает и как его применять в реальных вычислениях. Для понимания нам понадобится сложение, умножение, понимание того, что такое единичный вектор, единичная окружность, косинус, синус и немного воображения. Но оно и так будет понятно из примеров.
Вообщем если у вас тоже есть пробел в знаниях по теме произведения векторов то тут мы его закроем, а заодно узнаете пару тройку кейсов применения. Лично я оказался изрядно удивлен той простотой решения которую может дать такое на первый взгляд примитивное Скалярное произведение
(статья в процессе написания и добавления иллюстраций )
Графическое отображение скалярного произведения
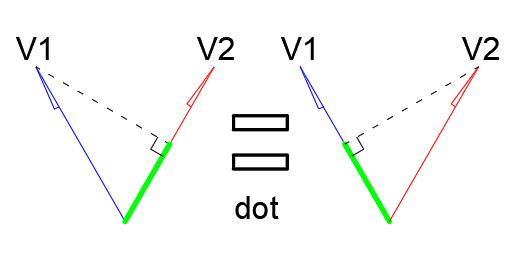
Итак у нас есть два вектора, Z ординату пока опустим, для понятности — V1 = (1,0) и V2 = (0,1) давайте найдем скалярное произведение (это значит координаты перемножим, а получившиеся произведения сложим, получив число — скалярное произведение), назовём его dot:
dot = V1.X*V2.X + V1.Y*V2.Y = 1*0 + 0*1 = 0
Ух ты — скалярное произведение равно нулю. Это как так?
А вот и наше первое и крайне важное свойство скалярного прозведения, если два вектора перпендикулярны их произведение равно нулю. И наоборот если скалярное произведение двух векторов даёт ноль — вектора перпендикулярны.
Для многих аналитических задач уже одно это свойство позволяет упростить решение. Например если у нас дана плоскость в виде точки и нормали, и надо найти пересечение с отрезком или прямой. Мы можем проверить, а они вообще в теории могут пересекаться-то?
Если векторное произведение нормали плоскости и вектора отрезка равно нулю — нет не могут.
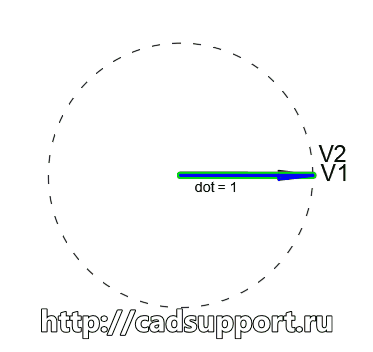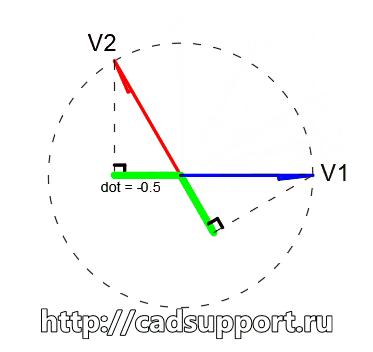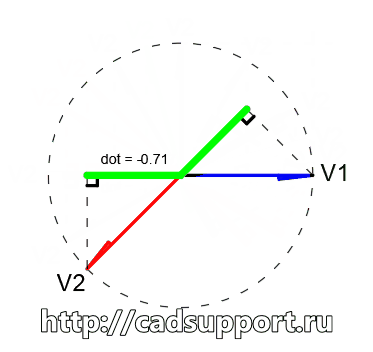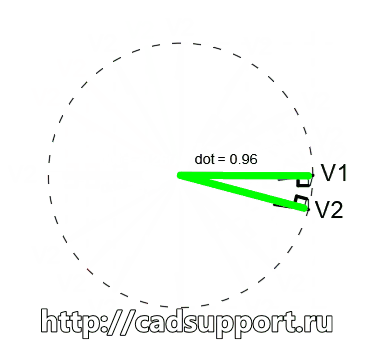
Пойдем дальше — изменим V2 = (0.707,0.707) — (единичный отрезок под углом 45 градусов)
dot = V1.X*V2.X + V1.Y*V2.Y = 0.707*1 + 0*0.707 = 0.707
Итак мы умножили два единичных вектора, и получили 0.707. Умножение двух единичных векторов дает нам косинус угла между между ними. В данном случае это косинус угла 45. А зная косинус мы можем найти и синус а значит и катеты треугольника который образуется этими векторами. Но это такое, свойство и из википедии понятное.
Геометрический смысл скалярного произведения
На этой анимации наглядно видно чему соответствует скаляр получаемый из двух единичных векторов. Его значение тут отложено зеленым вдоль каждого вектора. Скаляр — это просто число. Но его значение, для единичных векторов соответствует косинусу угла между этими векторами.
V2 = (-1, 1) (длинна этого вектора — корень из двух, что >1)
dot = V1.X*V2.X + V1.Y*V2.Y = -1*1 + 0*1 = -1
А тут у нас скалярное произведение стало отрицательным. О чем это нам говорит? Выше у нас был ноль — это перпендикуляр, т.е. 90 градусов. Потом было положительное число — 45 градусов, а теперь — отрицательное. Причем я специально не стал тут делать единичный вектор. Смысл этого примера в том, что зная положительный вектор или отрицательный — мы сразу можем сделать интересный ввывод о природе отношения этих векторов друг с другом.
На примере той же плоскости, зная нормаль и зная вектор от точки задающей плоскость до любой другой точки в пространстве, мы может уверенно сказать лежит ли точка по одну сторону с направлением нормали, или наоборот — она с другой стороны. Таким образом мы можем оставить только те точки которые лежат с одной или с другой стороны плоскости. А если точки лежат на плоскости — скалярное произведение будет равно нулю.
Зная только это — мы уже можем решать целый ряд задач.
Итак — зная знак произведения мы можем сказать кое, что об отношении векторов друг к другу.
Умножив два единичных вектора мы можем найти косинус угла между ними.
Скалярное произведение двух векторов простыми словами
Пусть теперь вектор V1 = (10, 5) , а вектор V2 = (10,10)
dot = V1.X*V2.X + V1.Y*V2.Y = 10*10 + 5*10 = 100+50=150
Вектора вроде не большие, а их скалярное произведение получилось здоровенным. Как так то? Что нам дает эта цифра? Что она вообще значит?
Это не похоже на векторное сложение и произведение. Это просто огромная цифра. Но каково её геометрическое значение?
Единичный вектор с единичным — дают косинус ( он же — прилежащий катет единичного вектора).
Единичный вектор с вектором больше или меньше единичного — дает длинну катета прямоугольного треугольника образованного этими двумя векторами. Иначе говоря — мы косинус угла между векторами умножили на длинну вектора, который не равен единице, и получили длинну катета. Это как на анимации выше — там два единичных вектора, и поэтому косинус умножить на единицу — всё равно косинус , а вот если один вектору у нас был равен пяти единичным векторам а другой единице — то единицу отбрасываем, а косинус умножаем на 5. Но прелесть в том что нам не надо это делать, достаточно посчитать скалярное произведение, и всё, значение катета у нас в кармане. Можем потом из этого значения найти и сам косинус поделив катет на длинну вектора.
Зная это теперь мы можем объяснить откуда в примере выше взялось такое несуразно огромное число. Неединичный вектор на неединичный вектор дает нам катет, но длинна его умножена на длинну вектора. Иначе говоря у нас есть V1 который равен 5 единичным векторам, и V2 который равен десяти единичным векторам. Так вот наше произведение нам даст такую штуку как если мы умножили два единичных вектора и получив косинус угла между ними — умножили его на длинну первого вектора, получив его катет, а потом этом катет умножили на длинну второго вектора.
Причем, так как это умножение и сложение, можно эти шаги переставлять местами, результат будет одинаков.
А главное — нам не нужно делать эти шаги. Достаточно посчитать скалярное произведение.
Примеры использования скалярного произведения
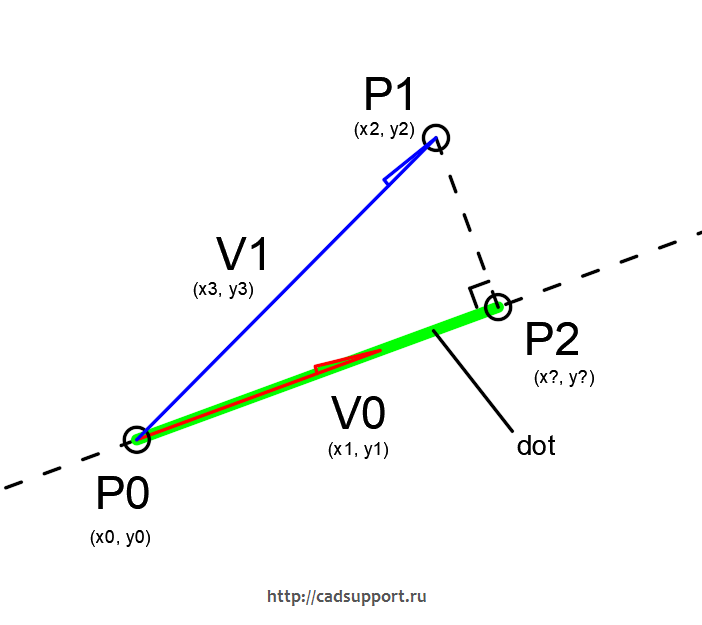 Что если у нас есть прямая заданная точкой (p0) и вектором (v0), и еще одна точка (p1), и надо найти координаты точки (p2) лежащей на этой прямой перпендикулярно к искомой точке. Или по другому — провести на прямую перпендикуляр из точки. Он же — кратчайшей расстояние между точкой и прямой.
Что если у нас есть прямая заданная точкой (p0) и вектором (v0), и еще одна точка (p1), и надо найти координаты точки (p2) лежащей на этой прямой перпендикулярно к искомой точке. Или по другому — провести на прямую перпендикуляр из точки. Он же — кратчайшей расстояние между точкой и прямой.
Зная выше описанные свойства скалярного произведения — задачка на три действия.
Найдем вектор из точки задающей прямую к искомой точке —
v1 = (X = p1.x-p0.x, Y = p1.y — p0.y)
Потом найдем скалярное произведение между v0 и v1
dot = v0.X*v1.X+v0.Y*v1.Y
И теперь нам осталось отложить из точки на прямой, вдоль вектора задающий прямую наше произведение, итак :
p2 = (X = v0.X*dot , Y = v0.Y*dot)
Ну и тут же мы можем сказать о том что если произведение равно нулю — то искомая точки — и есть точка с которая задаёт прямую.
А если скаляр меньше нуля — то значит точка находится позади точки задающей прямую.
Расстояние от точки до прямой это скалярное произведение
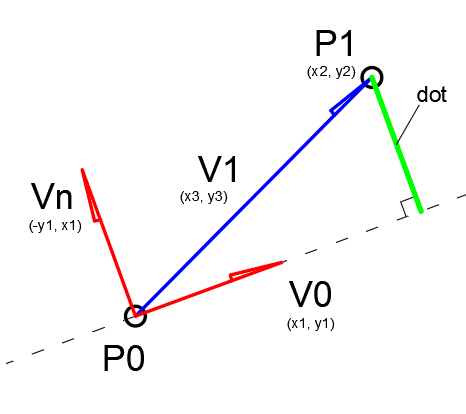 А что если нам не нужны координаты точки, но нужно расстояние от точки до прямой?
А что если нам не нужны координаты точки, но нужно расстояние от точки до прямой?
Еще проще!
Найдем вектор из точки задающей прямую к искомой точке —
v1 = (X = p1.x-p0.x, Y = p1.y — p0.y)
Потом найдем скалярное произведение между v0 и v1
dot = v0.X*v1.Y-v0.Y*v1.X
Всё, теперь наш скаляр дал нам искомое число. Правда в таком виде это подходит только для двух мерного пространства. Если вдруг вам не ясно с чего мы вдруг стали умножать икс на игрек, да и минус воткнули — это одно из свойство векторов в двух мерном пространстве — вектор перпендикулярный изветному можно найти поменяв икс и игрек местами, если перпендикуляр будем отсчитывать против часовой стрелки. Либо у икса поменять знак, если по часовой стрелке.
Кратчайшее расстояние от точки до плоскости
Итак есть плоскость задання с помощью точки (p0) в трехмерном пространстве и вектора нормали (n) плоскости. И есть точка (p1) заданная в виде координаты.
Кратчайшим расстоянием от точки до плоскости будет перпендикуляр опущенный из этой точки на эту плоскость. Если что — вектор этого перпендикуляра мы уже знаем — это наша нормаль.
А вот как найти расстояние?
Проведем вектор из точки задающей плоскость к искомой точке —
v = (X = p1.x-p0.x, Y=p1.y-p0.y, Z=p1.z-p0.z) = (X,Y,Z)
Итак есть вектор, есть нормаль. И… а собственно и все — ответом будет скаляр между этим вектором и нормалью.
dot = n.X*v.X + n.Y*v.Y+n.Z*v.Z
Потому что нормаль это перпендикуляр. Гипотенуза прямоугольника найденный вектор. А Скаляр этой гипотенузы и этого вектора даст длинну катета от искомой точки до плоскости.
2 комментария