Порывшись в этих самых интернетах, мне не удалось сходу найти аналитическое решение для тривиальной в принципе задачи: найти координаты точек касательных построенных из заданной точки на заданной же окружности. Точнее решения есть, но они в большинстве своем геометрические. Т.е. для программной реализации не годятся.

Предлагаемое решение не претендует на оригинальность или эффективность. А автор статьи не претендует на авторство, ибо и сам вероятно где-то его (решение или его часть) подглядел, но за давностью лет запамятовал где именно.

Основная цель данной статьи показать на примере как подобные задачи могут решаться в принципе. Сам алгоритм можно оптимизировать убрать лишние вычисления и шаги, а можно и вовсе решить задачу иначе. Однако в предлагаемом виде решение будет вполне понятно и не посвященному в таинства аналитической геометрии. Во всяком случае автор надеется на то, что столь подробное объяснение такой тривиальной задачи станет трамплином для тех кто дерзает проникнуть в тайны этой увлекательной науки.

Найдем координату точки касательной

Итак в нашей задаче будет 5 вводных параметров — это две координаты точки лежащей на плоскости — X и Y, еще две координаты это центр окружности — Xo, Yo. В принципе можно было бы обойтись и без них, приняв по умолчанию центр окружности за  начало координат, и тем самым пропустив пару шагов не имеющих решительно никакого значения для принципиального решения задач, однако пусть они будут. И пятый аргумент — радиус окружности.

Расстояние от центра окружности до точки

Тут все просто — вычитаем по парно координаты, возводим в квадраты эти разности, складываем и вычисляем корень. Получившийся результат в соответствии с теоремой Пифагора и будет нашим расстоянием между точками.

Главное свойство касательных к окружности

Касательной линией считается такая и только такая линия которая  в точке касания образует нормаль, т.е. перпендикуляр к кривой. В нашем случае окружности. В противном случае это уже будет не касательная а либо пересекающая линия, либо не соприкасающаяся.

Так как в нашей истории повился еще один прямой угол, в котором гипотенузой является наш отрезок между точкой и центром, а одним из катетов радиус — мы можем найти синус угла между отрезком и касательной из заданной точки. Для этого сделаем финт ушами и разделим радиус окружности на найденное расстояние.

Можно так же сказать что разделив радиус на длину касательной мы получим одну из ординат в системе координат заданной этими векторами(радиус и касательная).

Вторую ординату, она же косинус угла между отрезом и касательной получим через теорему Пифагора — корень из разности единицы и квадрата известной ординаты.

Длина отрезка касательной построенной из точки

Теперь умножив расстояние между точками на вторую ординату мы найдем длину касательной. Что делает нас на шаг ближе к искомым координатам. Длинны отрезков касательных к окружности будут равны друг другу в любых случаях.

Координаты точки касания

Собственно всё, что нам нужно для того чтобы найти координаты точки у нас уже есть. Если объяснять на пальцах, то теперь нам надо повернуть вектор заданный точкой и центром окружности на угол альфа, синус и косинус которого нам уже известны. И отложить на новом векторе длину касательной.

Только отложим мы её через оридинаты. Для этого уменьшим каждую ординату на косинус угла — itg, таким образом мы получим ординаты отрезка лежащего на векторе между точкой и центром, с длинной равной нашей касательно. А потом повернем на угол между касательной и отрезком домножив на косинус и синус угла.

Xt2 = Dy*itg*jtg — itg*itg*Dx

Yt2 = -itg*Dy*itg — jtg*Dx*itg

 

Теперь разберем все на примере.

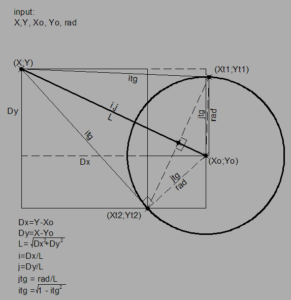
Dx = X-Xo

Dy = Y-Yo

L=SQRT ( Dx*Dx+Dy*Dy)

jtg = Rad/ L

itg = SQRT (1 — jtg*jtg)

Xtg = -itg*Dx*itg + itg*Dy*jtg

Ytg = -itg*Dx*jtg — itg*Dy*itg

 

Координаты точки касательной C#

Собственно теперь перейдем от словословий к делу, ниже приведен код в котором применены рассуждения выше. Пять аргументов на входе, две координаты на выходе. Саму функцию можно вероятно оптимизировать слив все промежуточные шаги в один, но в таком виде, с учетом вышеизложенных рассуждений, будет по крайней мере понятно откуда какие коэффициенты взялись и что именно они делают в алгоритме.

        public double[] GetTangentPointCoordinate(double X, double Y, double Xo, double Yo, double rad)
        {
            double dx = X - Xo; double dy = Y - Yo;
            double L = Math.Sqrt(dx * dx + dy * dy);
            double itg = rad / L;
            double jtg = Math.Sqrt(1 - itg * itg);
            double Xtg = -itg * dx * itg + itg * dy * jtg;
            double Ytg = -itg * dx * jtg - itg * dy * itg;
            return new double[] { Xtg, Ytg };
        }

Угол между двумя касательными к окружности

Ну а теперь развлечемся, и так сказать закрепим материал. Угол между двумя касательными мы можем найти разделив радиус окружности на длину отрезка между точкой из которой мы строим касательные и центром окружности. Таким образом благодаря свойству перпендикулярности мы получим синус угла между касательной и отрезком. Осталось взять арксинус и умножить его на два. Угол будет иметь следующий вид

alfa = 2 * arcsin(rad/L)